نظرسنجی
دستهها
- پروژه های آماده
- ترجمه تخصصی متون برق
- تدریس دروس
- جزوات آموزشی
- دانلود رایگان پروژه
- معرفی و دانلود کتاب
- انرژی های نو
- الکترونیک قدرت
- عمومی
- تلگرام
- ماشین های الکتریکی
- تئوری جامع ماشین های الکتریکی
- کنترل فازی
- مقالات برق قدرت
- نرم افزار برق قدرت
- متلب
- طراحی مبدل الکترونیک قدرت
- کنترل خطی
- الگوریتم های تکاملی
- سیستم های قدرت
- کنترل مدرن
- شبکه شکل دهی پالس
- سوییچ تایراترون
ابر برجسب
پایان نامه توربین بادی برق پروژه درس تئوری الکترونیک قدرت پروژه الکترونیک قدرت 2 توربین بادی پروژه مقاله ISI طراحی برد مدار چاپی طراحی PCB آموزش دیگسایلنت همانندجویی انرژی تجدیدپذیر کنترل میکروگرید شبیه سازی متلب پردازش سیگنال شبیه سازی انرژی خورشیدی انرژی باد سنسور پایان نامه الکترونیک قدرت رله دانلود رایگان ترانس جریان چیستان پنل خورشیدی مقاله برق قدرت مقاله برق استخراج مقاله از پایان نامه اصلاح همانندجویی مبدل الکترونیک قدرت بیت کوین شبکه قدرت کنترل ولتاژ پروپوزال ثبت پایان نامه کنترل فازی پایان نامه مخابرات پایان نامه کنترل کرکره برقی کنترل مدرن کنترل تطبیقی متلب انرژی تئوری جامع ماشین الکتریکی پروژه تئوری جامع ماشین الکتریکی انرژی برق شبیه سازی dfig دانلود پایان نامه توربین بادی شبیه سازی برق قدرت انجام پایان نامه برق درایو ترانسفورماتور تاسیسات الکتریکی سوالات مصاحبه آزمون استخدامی موتور القایی ماشین القایی ابزار دقیق میکروکنترلر پروژه دیگسایلنت کاهش درصد همانندجویی پایان نامه میکروگرید پایان نامه ریزشبکه انرژی نو اینورتر پایان نامه دیگسایلنت چاپ مقاله ارز دیجیتال سامانه همانندجو شبیه سازی مقاله برق کنترل مهندسی برق قدرت الکتروموتور شبیه سازی با متلب انجام پایان نامه انجام پایان نامه برق قدرت شبیه سازی دیگسایلنت همانندجو ریزشبکه پروژه طراحی مبدل الکترونیک قدرت سیستم قدرت پروژه الکترونیک قدرت معما مبدل سوییچینگ مقاله میکروگرید دیگسایلنت مهندسی برق توربین بادی dfig طراحی مبدل سوییچینگ دانلود رایگان پایان نامه شبیه سازی مقاله برق قدرت شبیه سازی توربین بادی شبیه سازی مقاله پایان نامه برق الکترونیک پایان نامه برق قدرت پایان نامه پایان نامه برق برق قدرتبرگهها
جدیدترین یادداشتها
همه- "شبیهسازی پیشرفته با MATLAB: خدمات تخصصی پروژههای مهندسی
- شبیهسازی مدارهای الکترونیکی با PSPICE
- انجام پایاننامه و پروپوزال در تمامی رشتههای دانشگاهی
- انجام پایاننامه و مقالهنویسی روانشناسی
- آمادهسازی یک پروپوزال قوی و حرفهای
- طراحی پاورپوینت حرفهای برای روز دفاع
- توربینهای بادی DFIG: قلب تپنده انرژی بادی مدرن
- خودروهای برقی: آینده حمل و نقل با تکنولوژیهای پیشرفته
- صفر تا صد انجام پایاننامه: راهنمای جامع از انتخاب موضوع تا دفاع موفق
- رساله دکترای مهندسی برق
- کاهش درصد شباهت متن با پارافریز حرفهای
- پایاننامه (مقاله ) در حوزه کنترل ماشینهای سنکرون و آسنکرون
- پایاننامه (مقاله) درباره مبدلهای DC-DC
- خدمات تخصصی انجام پایاننامه و نگارش مقاله در رشته مهندسی برق گرایش الکترونیک
- خدمات تخصصی انجام پایاننامه و نگارش مقاله در رشته مهندسی برق گرایش مخابرات
تقویم
فروردین 1404| ش | ی | د | س | چ | پ | ج |
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 | 31 |
جستجو
تبدیل ستاره مثلث
شبکهها یا مدارهای سهفاز استاندارد، دو فرم اصلی دارند که بیانگر نوع
اتصال آنها است. یک شبکه اتصال «ستاره» (Star) که با حرف Y نمایش داده
میشود و یک اتصال «دلتا» (Delta) یا «مثلث»، که با نماد مثلث یا
آن را نشان میدهیم.
اگر یک منبع سهفاز سهسیمه یا بار سهفاز داشته باشیم، میتوانیم به سادگی آن را با استفاده از تبدیل ستاره به مثلث یا مثلث به ستاره، به اتصال معادل دیگر تبدیل کنیم.
یک شبکه مقاومتی متشکل از سه امپدانس را که به فرم یک پیکربندی T متصل شدهاند، میتوان به شکل ستاره یا Y زیر بازنویسی کرد:
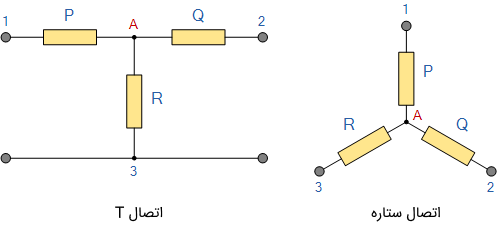
همچنین میتوان یک شبکه مقاومتی نوع
را به صورت معادل الکتریکی مثلث نوشت:
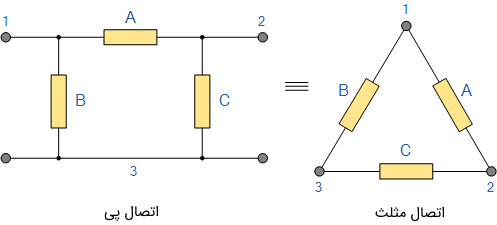
تبدیل ستاره به مثلث و مثلث به ستاره، با استفاده از رابطه ریاضی بین مقاومتهای مختلف آنها انجام میشود. این تبدیلات مداری، ما را قادر میسازند که مقاومتها (امپدانسها)ی اتصال را با معادل آنها بین سرهای 2-1، 3-1 یا 3-2 به صورت ستاره یا مثلث بیان کنیم. هرچند ولتاژ و جریان سرهای خروجی دو شبکه اصلی و تبدیل شده در دو حالت برابر است، اما ولتاژها و جریانهای داخلی شبکه اصلی نسبت به معادل آن متفاوت است. با این اوصاف، شبکه اصلی و معادل، توان یکسانی مصرف میکنند.
تبدیل مثلث به ستاره
برای تبدیل یک شبکه مثلث به معادل ستاره، لازم است فرمول تبدیل را برای معادلسازی مقاومتهای مختلف بین هر دو سر شبکه به دست آوریم. شکل زیر را در نظر بگیرید.
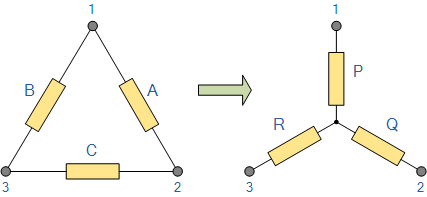
به مقاومتهای بین دو سر 1 و 2 توجه کنید.
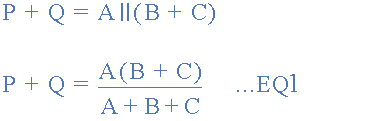
ادامه موضوع در بخش ادامه مطلب
مقاومتهای بین دو سر 2 و ۳ نیز به صورت زیر هستند:
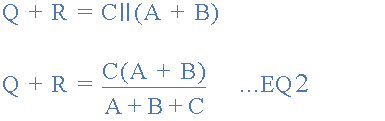
برای مقاومتهای بین دو سر 1 و ۳ نیز داریم:
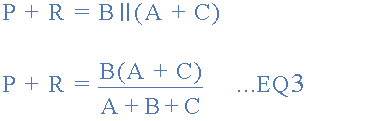
با توجه به روابط بالا، سه معادله داریم. با تفریق معادله 2 از معادله 3 داریم:

در نتیجه، میتوانیم معادله ۱ را به صورت زیر بازنویسی کنیم:
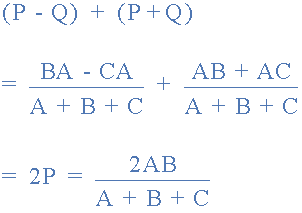
با جمع کردن معادله بالا و معادله قبل از آن، داریم:
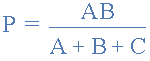
بنابراین مقدار مقاومت P را میتوانیم با فرمول زیر به دست آوریم.
برای خلاصه میتوان گفت که معادله 1 با (رابطه2 – رابطه3 + رابطه1) محاسبه میشود.
به طریق مشابه، مقاومت Q اتصال ستاره از مجموع جبری (رابطه3 – رابطه1 + رابطه2) به دست میآید:
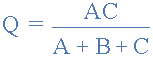
و در نهایت، مقاومت R را نیز می توان با (رابطه1 – رابطه2 + رابطه3) محاسبه کرد:

مخرج همه فرمولهای تبدیل مثلث به ستاره، A+B+C است که بیانگر مجموع مقاومتهای اتصال مثلث خواهد بود.
خلاصه معادلههای تبدیل مثلث به ستاره در فرمول زیر آورده شده است:
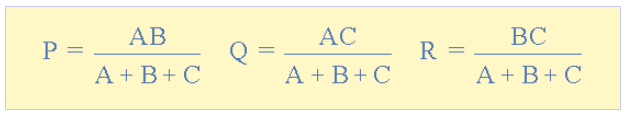
اگر سه مقاومت اتصال مثلث با هم برابر باشند، مقاومت معادل در اتصال
ستاره، یک سوم مقدار هر یک از آنها خواهد بود. به عبارت دیگر، هر شاخه
مقاومتی اتصال ستاره برابر خواهد بود با:
.
مثال 1
معادل ستاره شبکه مثلث زیر را به دست آوردید.
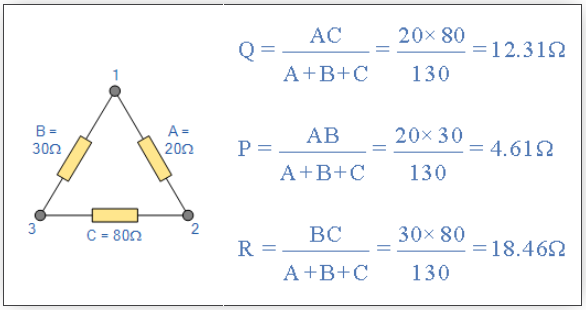
تبدیل ستاره به مثلث
تبدیل ستاره به مثلث، عکس تبدیل مثلث به ستاره است که آن را بیان کردیم. دیدیم که مقاومت متصل به یک ترمینال در اتصال ستاره، از ضرب دو مقاومت متصل به همان ترمینال در پیکربندی مثلث به دست میآید.
با بازنویسی فرمولهای بالا، میتوانیم تبدیلات ستاره به مثلث را محاسبه کنیم.
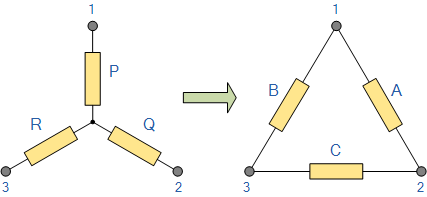
مقدار هر مقاومت روی هر ضلع اتصال مثلث برابر است با مجموع ضرب ترکیبات دو به دوی اتصال ستاره تقسیم بر مقاومتی که به رأس مقابل این ضلع متصل است. بنابراین، فرمول محاسبه مقاومت A به شکل زیر است:

به همین ترتیب، مقاومتهای متصل بین سرهای 1 و 3 و همچنین 2 و 3 به صورت زیر نوشته میشود:
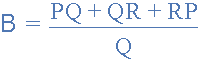
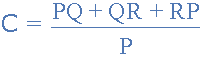
با تقسیم جداگانه هر عبارت از صورت کسر سه فرمول اخیر، میتوانیم آنها را به صورت زیر بازنویسی کنیم:
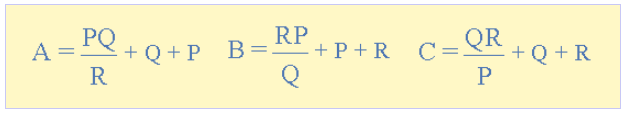
اگر همه مقاومتهای اتصال ستاره با هم برابر باشند، مقاومتهای معادل
اتصال مثلث آن، سه برابر هر یک از این مقاومتها خواهند بود. به عبارت
دیگر،
.
مثال 2
معادل مثلث شبکه ستاره زیر را به دست آوردید.
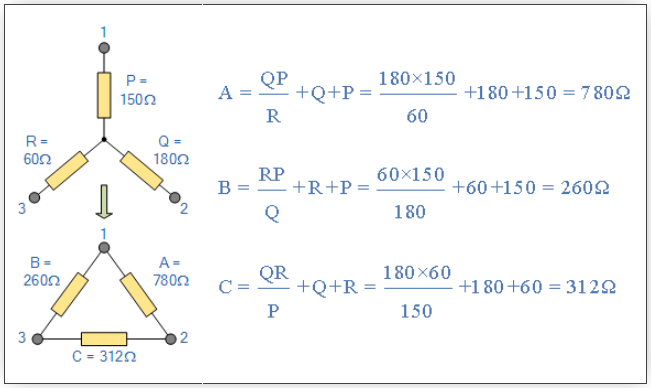
با کمک هر دو تبدیل ستاره به مثلث و مثلث به ستاره میتوانیم مدار را سادهتر کرده و آن را آسانتر تحلیل کنیم.

